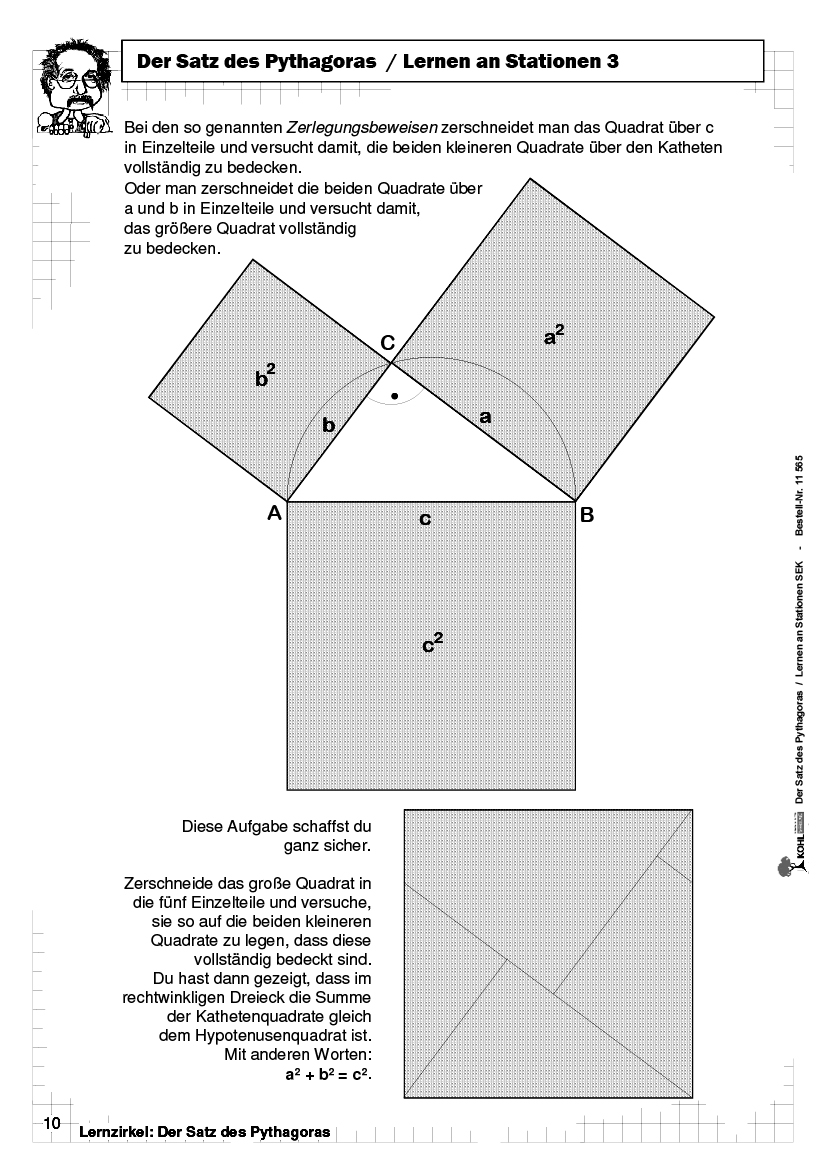
Der Satz des Pythagoras PDF, 96 S. 4learning2gether.eu
Aufgaben: Satz des Pythagoras Lösungen: a) x = 6,36 cm; 52,92 m 2,24 m a) 288 m 98,22 m 4,24 cm b) y = 1,5 cm; b) 340 m c) z = 4,8 cm mehr auf www.real-mathematik.de
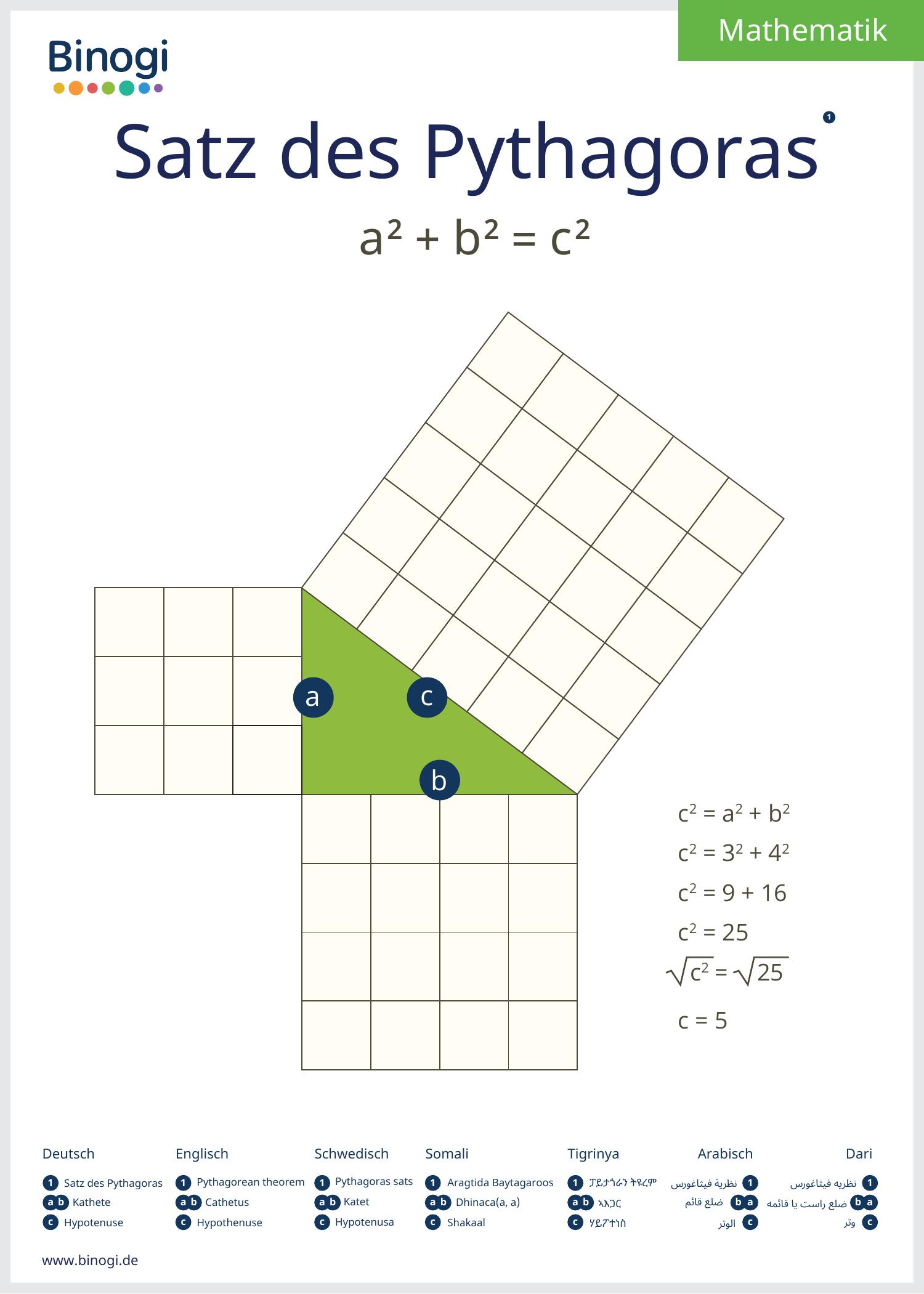
Satz_des_Pythagoras.pdf DocDroid
Satz des Pythagoras Der SatzdesPythagorasbesagt dassbeieinemrechtwinkligenDreieck die Quadrate überdenKathetenzusammengenaudie selbeFlächehaben wiedasQuadratüberderHypotenuse oftb 2 b ? b- a a C a)b± Katheten (schließendenrechten Winkelein) Üc EHypotenuse(liegtdemrechtenWinkel gegenüber) Kathete tKathete =Hypotenuse a Beispiel1:geg :a =4cmges:c
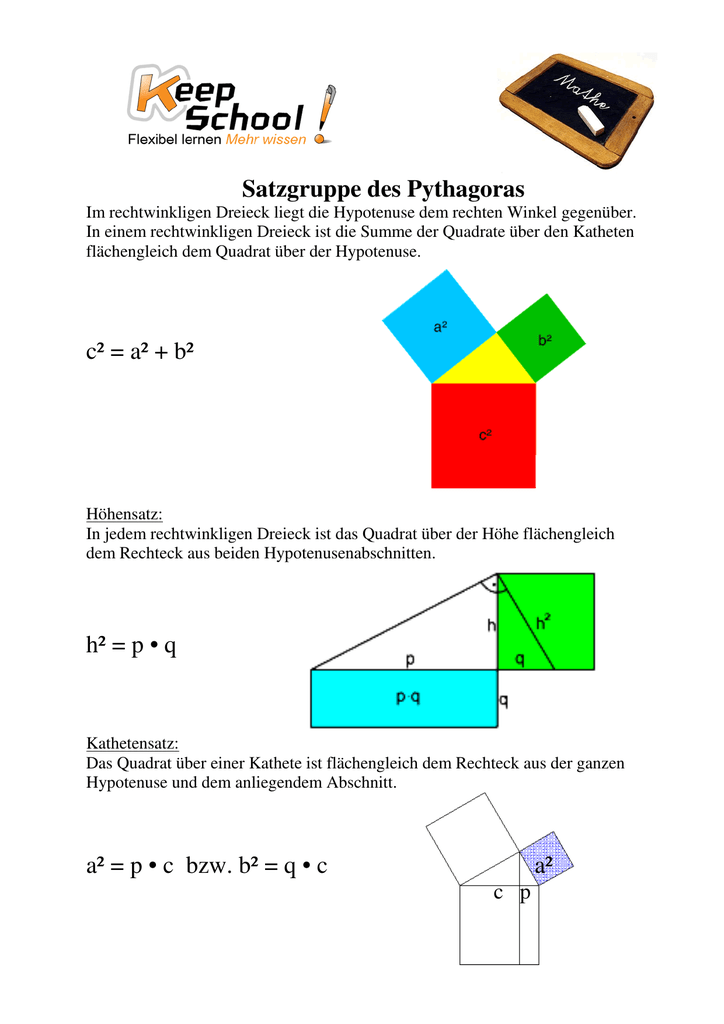
Satzgruppe des Pythagoras als pdf file
Lehrern mit 4,86/5 Sternen bewertet. 47 PDF-Dateien mit über 5000 Seiten inkl. 1 Jahr Updates für nur 29,99 €. Ab dem 2. Jahr nur 14,99 €/Jahr. Kündigung jederzeit mit wenigen Klicks. Erklärungen Geometrie Geometrische Figuren Dreieck Dreiecksarten Rechtwinkliges Dreieck Satz des Pythagoras Satz des Pythagoras
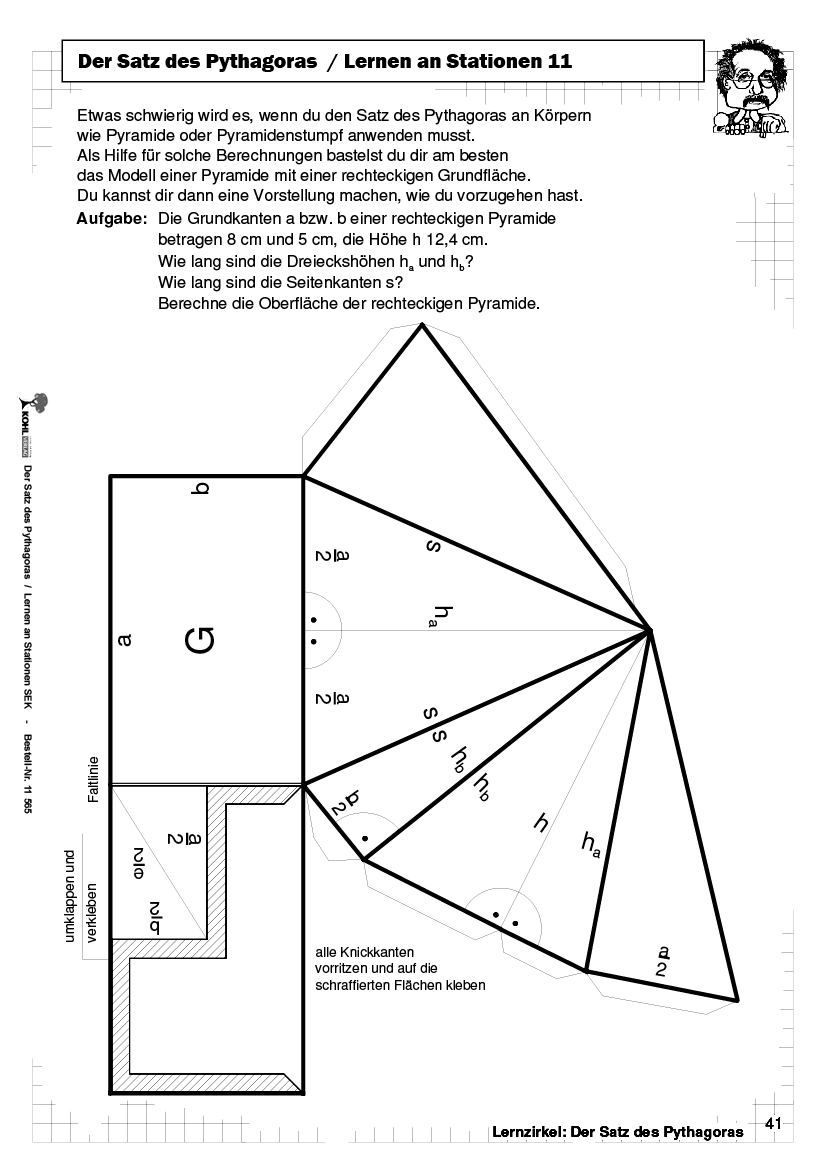
Der Satz des Pythagoras PDF, 96 S. 4learning2gether.eu
Übungsbeispiele zum Satz des Pythagoras 4. Klasse Berechne die fehlenden Seiten eines rechtwinkligen Dreiecks mit der Hypotenuse c und den Katheten a und b. Wenn das Ergebnis nicht ganzzahlig ist, runde auf zwei Dezimalstellen! a = 5 cm , c = 13 cm a = 9 cm , b = 12 cm b = 15 mm , c = 17 mm
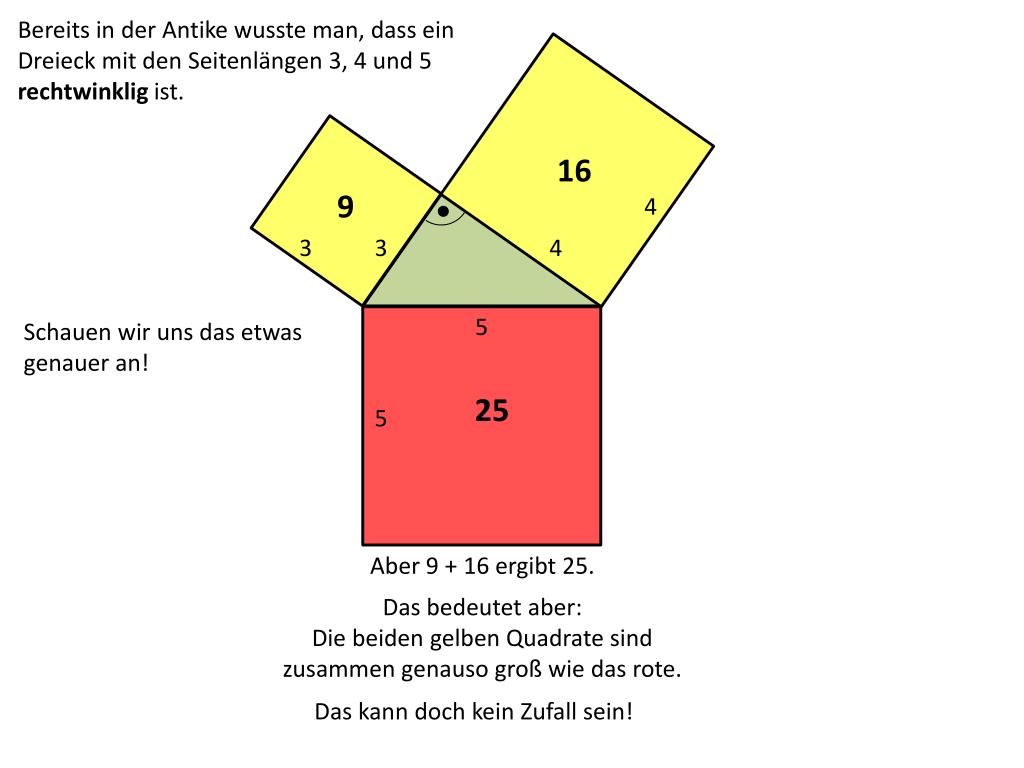
PPT Der Satz des Pythagoras PowerPoint Presentation, free download ID1905125
2.8. Prüfungsaufgaben zum Satz des Pythagoras Aufgabe 1: Rechtwinkliges Dreieck Ein rechtwinkliges Dreieck mit der Kathete a = 0,5 m hat die Fläche A = 2000 cm 2. Berechne die restlichen Seitenlängen dieses Dreiecks. Lösung 2000 cm 2 = 1 2 ·50 cm ·b b = 80 cm und c = (50 cm) (80 cm)2 2+ = ≈ 9,43 cm Aufgabe 2: Raute

Satz Des Pythagoras Aufgaben Mit Lösung PDF
Satz des Pythagoras Arbeitsblätter mit Übungen und Aufgaben zum Satz des Pythagoras für Mathe in der 9. Klasse am Gymnasium - mit Lösungen! Welche nützlichen Begriffe braucht man für den Satz des Pythagoras? In einem rechtwinkligen Dreieck gibt es immer eine Hypotenuse und zwei Katheten.
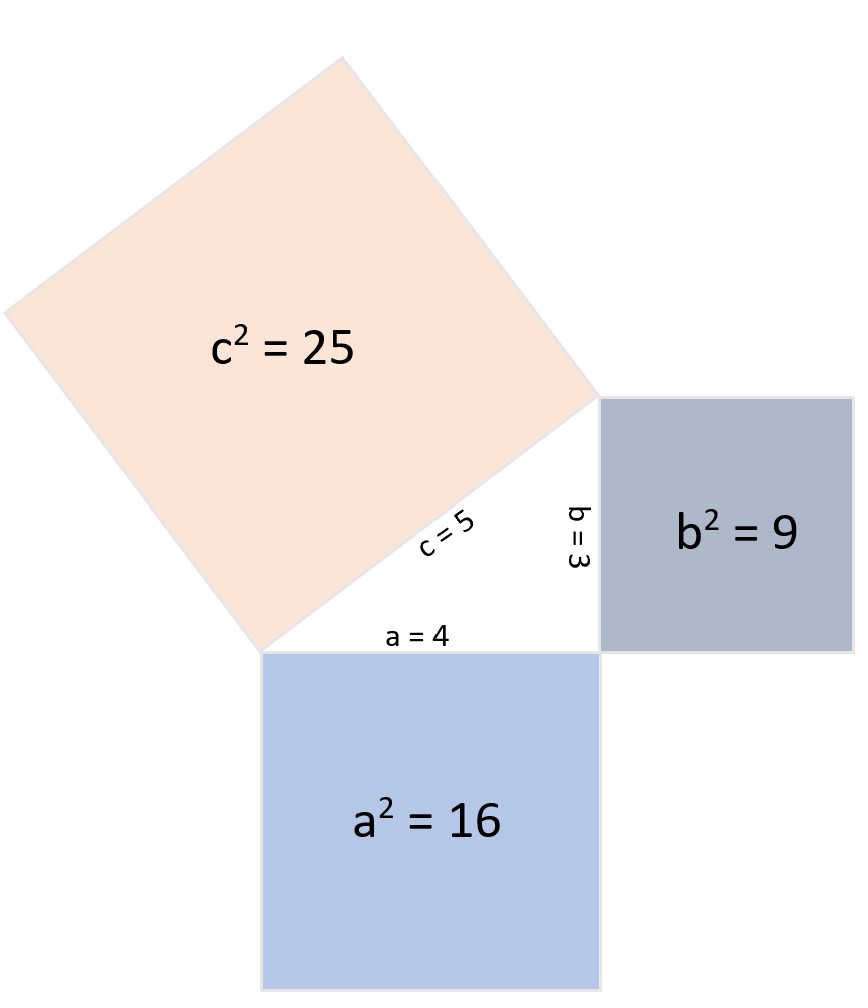
Satz des Pythagoras Die einfache SchrittfürSchrittAnleitung
Satz des Pythagoras Realschule / Gymnasium Klasse 9 Alexander Schwarz www.mathe-aufgaben.com Dezember 2014 Aufgabe 1: Berechne die Länge der fehlenden Seite. Aufgabe 2: Peter hat sich eine Leiter gekauft, die er beim Anstreichen seiner Hauswand benötigt.

Satz des Pythagoras Satz des pythagoras, Interaktives lernen, Rechtwinkliges dreieck
Pythagoras | (1)(1) Satz des Pythagoras : Ist ein Dreieck rec htwinklig , haben die Quadrate über den K ath eten zusammen denselben Fläch eni nhalt wie das Quadrat über der H ypote nuse . Werden die beiden K ath eten mit a und b und die H ypote nuse mit c bezeichnet, gilt: + =
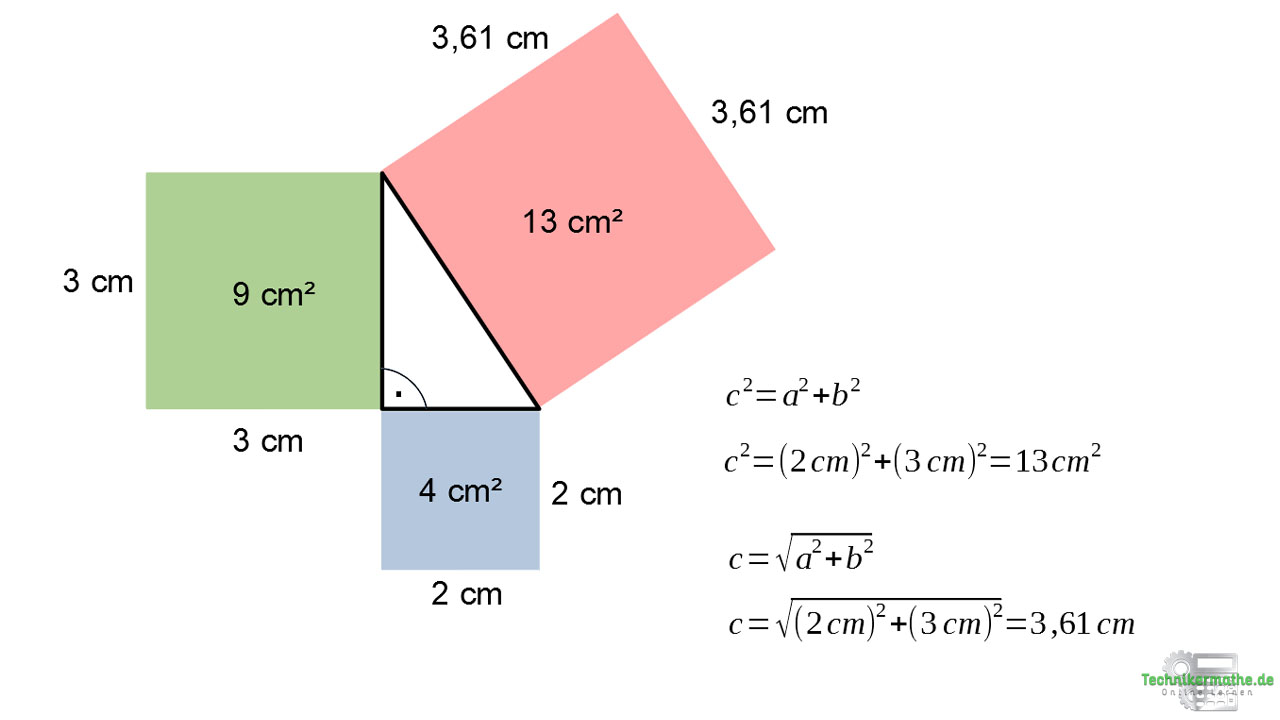
[INFO3] PH1 Satz des Pythagoras (inkl. Video) Technikermathe
(00:11) Der Satz des Pythagoras stellt in einem rechtwinkligen Dreieck eine Beziehung zwischen den drei Seiten a, b und c her. Rechtwinkliges Dreieck Satz des Pythagoras Formel In einem rechtwinkligen Dreieck gilt a ² + b ² = c² . Dabei sind a und b die beiden kurzen Seiten und c ist die lange Seite.
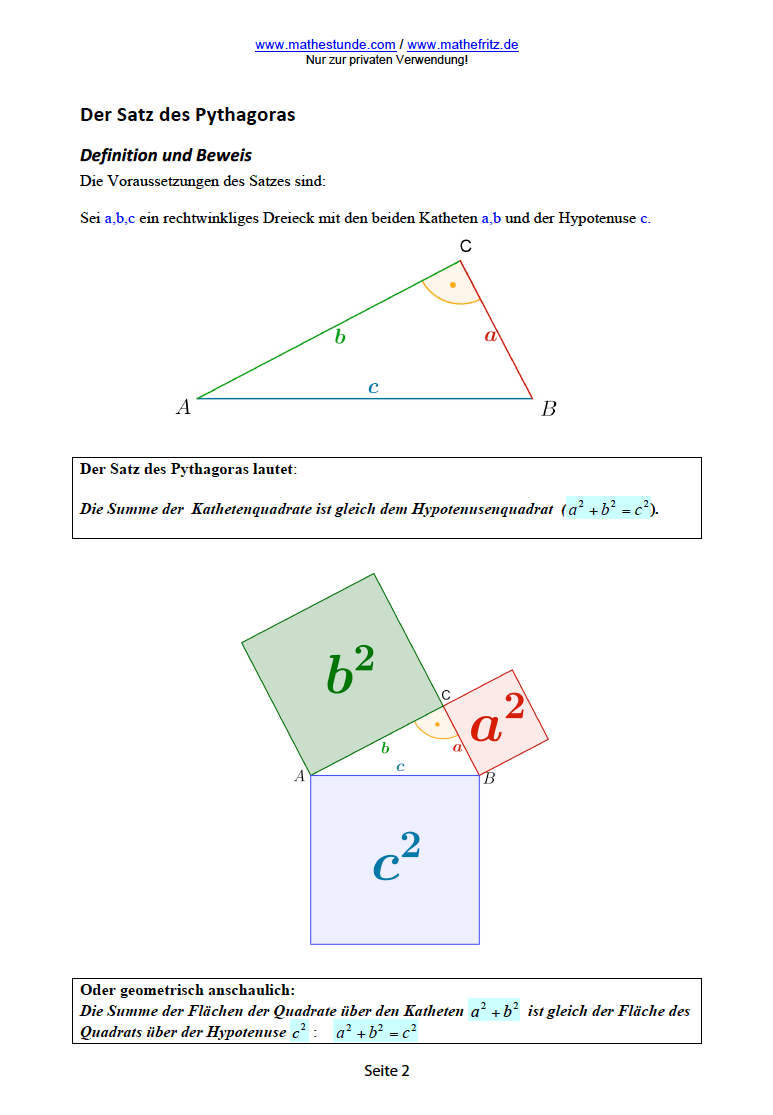
Satz des Pythagoras Aufgaben und Herleitung Pythagoras
Klasse. Kurs: 8. Klasse > Lerneinheit 5. Lektion 3: Satz des Pythagoras. Einführung in den Satz des Pythagoras. Satz des Pythagoras - Beispiel. Satz des Pythagoras - Einführungsaufgaben. Verwende den Satz des Pythagoras um Seitenlängen bei rechtwinkligen Dreiecken zu bestimmen. Anwendung des Satzes des Pythagoras bei gleichschenkligen Dreiecken.
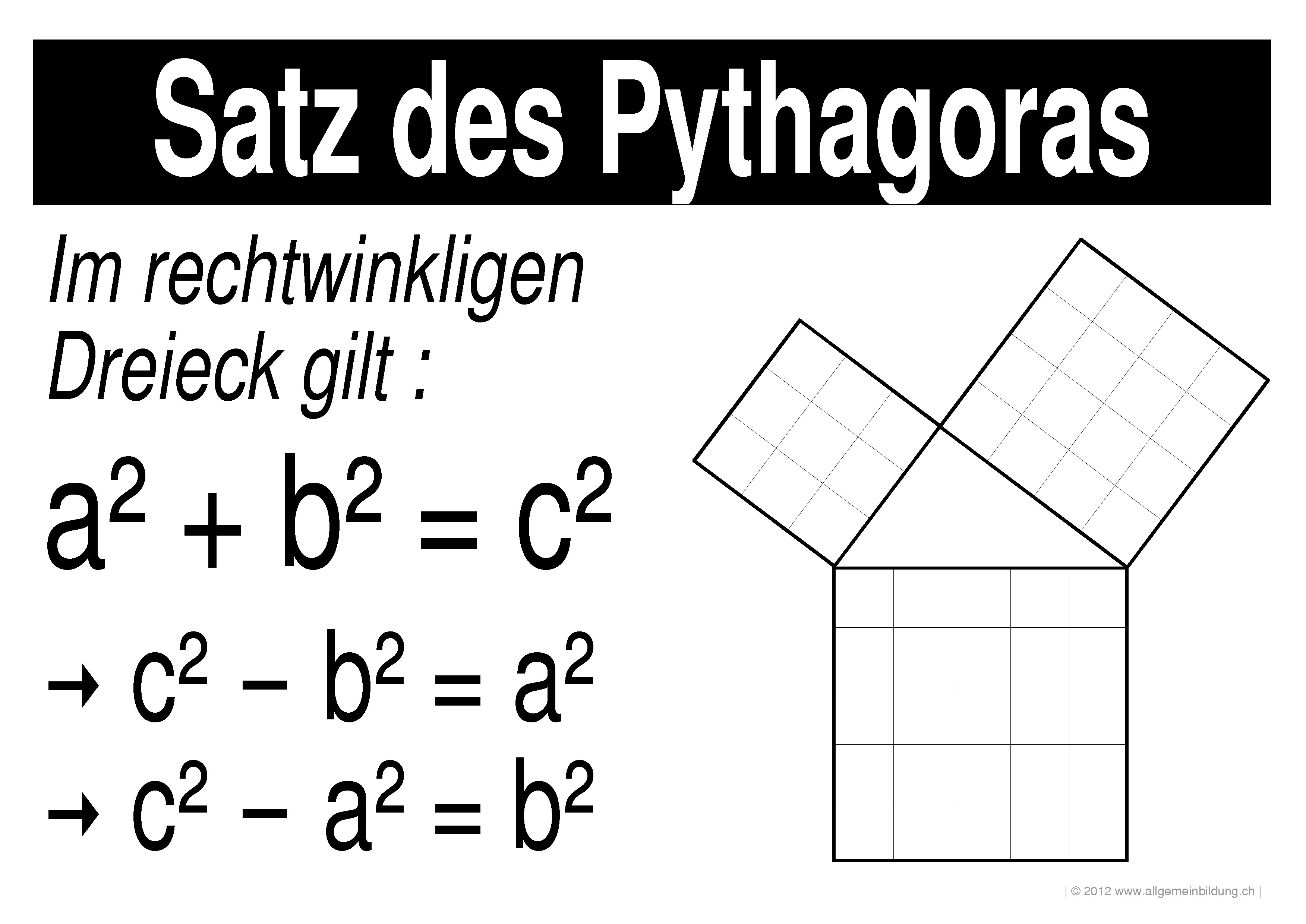
Satz des Pythagoras gratis Mathematik/GeometrieLernplakat WissensPoster 8500 kostenlose
7. Das Dach eines Einfamilienhauses hat die Form eines rechtwinkligen Dreiecks. Bei der Planung des Dachgebälks hat der Zimmermann folgende Vorgaben: p = 8,0 m, s = 12,5 m und h = 6,0 m. b Berechnen Sie die beiden Längen a und b. p h a s www.matheaktiv.de
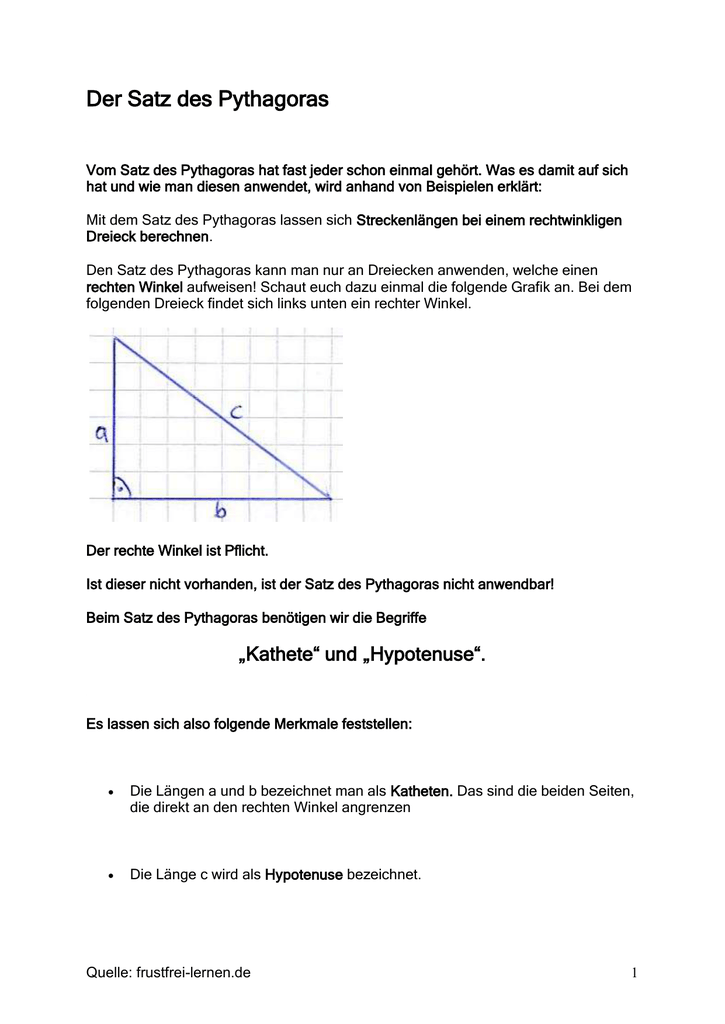
Der Satz des Pythagoras
Der Satz des Pythagoras als einer der berühmtesten Sätze der Mathematik hat seinen Ruf verdient. Er gehört zu den herausragendsten Beispielen für tiefe mathematische Kenntnisse früher Hochkulturen in Indien, Griechen-land und China (Schreiber 2000). In der Schulmathematik kennt man schon seit langem viele Zugänge und Be-weise.

D Fannie Poole Satz Des Pythagoras Formel
Der Satz des Pythagoras Dieser berühmte Lehrsatz der Mathematik soll der Geschichtsschreibung nach von Pythagoras von Samos (580 - 500 v.Chr.) entdeckt worden sein. Der Satz besagt, dass in einem rechtwinkligen Dreieck die Summe der beiden Katheten-Quadrate gleich dem Quadrat der Hypotenuse ist. Hypotenuse Es gilt also: 2 a + b 2 = 2 c
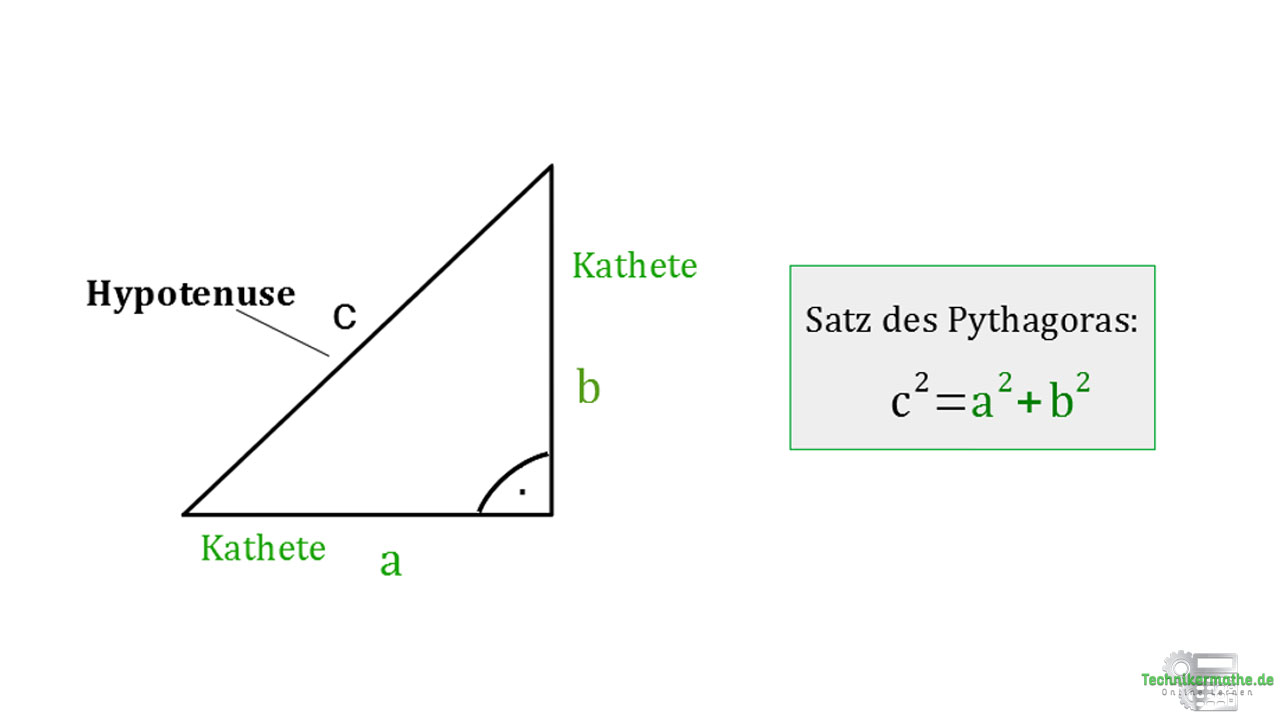
Satz des Pythagoras Einfach 1a erklärt [Video & Beispiele]
Satz von Pythagoras anwenden Achte darauf: 1. Du kannst im rechtwinkligen Dreieck mit zwei gegebenen Seiten die dritte berechnen (Aufgabe 1, 3). 2. Du kannst im Koordinatensystem Strecken mit Hilfe des Satzes von Pythagoras berechnen (Aufgabe 2). 3. Du kannst in Textaufgaben den Satz des Pythagoras anwenden (Aufgabe 4). 4.

Der Satz des Pythagoras PDF, 96 S. 4learning2gether.eu
Aufgaben zum Satz des Pythagoras Aufgabe 1 Vervollständige die folgende Tabelle: Aufgabe 2 Berechne jeweils die Länge der dritten Seite: Aufgabe 3 Zeichne die Punkte P und Q jeweils in ein Koordinatensystem mit der Längeneinheit 1 cm ein und bestimme ihren Abstand durch Zeichnung und Rechnung. a) P(2∣1) und Q(5∣5) b) P(−3∣4) und Q(2∣−1)
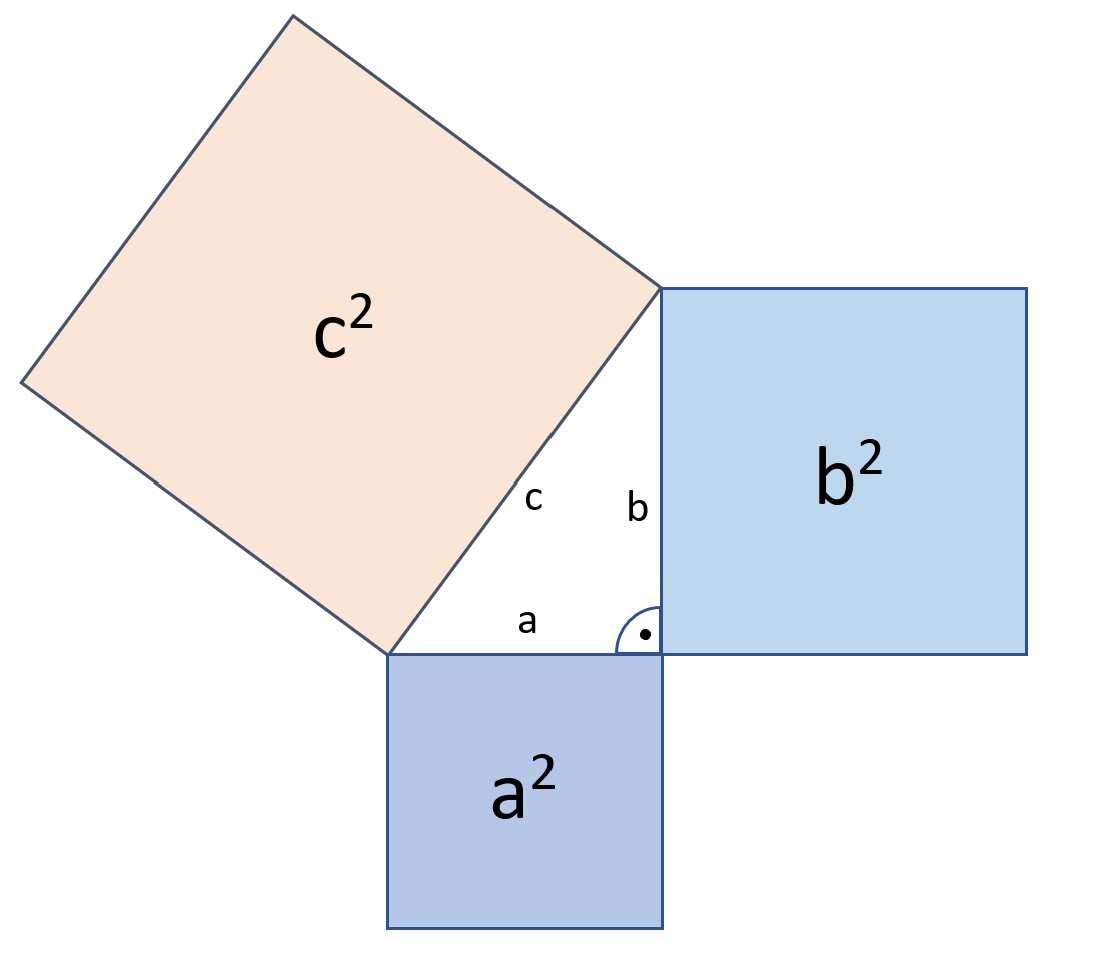
Satz des Pythagoras Die einfache SchrittfürSchrittAnleitung
Satz des Pythagoras in der Geometrie einfach erklärt: Definition Anwendung Berechnung Beispiele Video - simpleclub Mathematik